Vgreen class

Provides capabilities for pointwise evaluation of free space Green's function for point charges in a uniform dielectric. More...

Data Structures
struct	sVgreen
	Contains public data members for Vgreen class/module. More...
Files
file	vgreen.h
	Contains declarations for class Vgreen.
file	vgreen.c
	Class Vgreen methods.
Typedefs
typedef struct sVgreen	Vgreen
	Declaration of the Vgreen class as the Vgreen structure.
Functions
Valist *	Vgreen_getValist (Vgreen *thee)
	Get the atom list associated with this Green's function object.
unsigned long int	Vgreen_memChk (Vgreen *thee)
	Return the memory used by this structure (and its contents) in bytes.
Vgreen *	Vgreen_ctor (Valist *alist)
	Construct the Green's function oracle.
int	Vgreen_ctor2 (Vgreen thee, Valist alist)
	FORTRAN stub to construct the Green's function oracle.
void	Vgreen_dtor (Vgreen **thee)
	Destruct the Green's function oracle.
void	Vgreen_dtor2 (Vgreen *thee)
	FORTRAN stub to destruct the Green's function oracle.
int	Vgreen_helmholtz (Vgreen thee, int npos, double x, double y, double z, double *val, double kappa)
	Get the Green's function for Helmholtz's equation integrated over the atomic point charges.
int	Vgreen_helmholtzD (Vgreen thee, int npos, double x, double y, double z, double gradx, double grady, double *gradz, double kappa)
	Get the gradient of Green's function for Helmholtz's equation integrated over the atomic point charges.
int	Vgreen_coulomb_direct (Vgreen thee, int npos, double x, double y, double z, double *val)
	Get the Coulomb's Law Green's function (solution to Laplace's equation) integrated over the atomic point charges using direct summation.
int	Vgreen_coulomb (Vgreen thee, int npos, double x, double y, double z, double *val)
	Get the Coulomb's Law Green's function (solution to Laplace's equation) integrated over the atomic point charges using direct summation or H. E. Johnston, R. Krasny FMM library (if available).
int	Vgreen_coulombD_direct (Vgreen thee, int npos, double x, double y, double z, double pot, double gradx, double grady, double gradz)
	Get gradient of the Coulomb's Law Green's function (solution to Laplace's equation) integrated over the atomic point charges using direct summation.
int	Vgreen_coulombD (Vgreen thee, int npos, double x, double y, double z, double pot, double gradx, double grady, double gradz)
	Get gradient of the Coulomb's Law Green's function (solution to Laplace's equation) integrated over the atomic point charges using either direct summation or H. E. Johnston/R. Krasny FMM library (if available).

Detailed Description

Provides capabilities for pointwise evaluation of free space Green's function for point charges in a uniform dielectric.

Note:: Right now, these are very slow methods without any fast multipole acceleration.

Attention:

 *
 * APBS -- Adaptive Poisson-Boltzmann Solver
 *
 * Nathan A. Baker (baker@biochem.wustl.edu)
 * Dept. of Biochemistry and Molecular Biophysics
 * Center for Computational Biology
 * Washington University in St. Louis
 *
 * Additional contributing authors listed in the code documentation.
 *
 * Copyright (c) 2002-2009, Washington University in St. Louis.
 * Portions Copyright (c) 2002-2009.  Nathan A. Baker
 * Portions Copyright (c) 1999-2002.  The Regents of the University of California.
 * Portions Copyright (c) 1995.  Michael Holst
 *
 * All rights reserved.
 * 
 * Redistribution and use in source and binary forms, with or without
 * modification, are permitted provided that the following conditions are met: 
 *
 * -  Redistributions of source code must retain the above copyright notice, this
 * list of conditions and the following disclaimer.  
 * 
 * - Redistributions in binary form must reproduce the above copyright notice,
 * this list of conditions and the following disclaimer in the documentation
 * and/or other materials provided with the distribution.
 * 
 * - Neither the name of Washington University in St. Louis nor the names of its
 * contributors may be used to endorse or promote products derived from this
 * software without specific prior written permission.
 * 
 * THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS
 * "AS IS" AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT
 * LIMITED TO, THE IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR
 * A PARTICULAR PURPOSE ARE DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT OWNER OR
 * CONTRIBUTORS BE LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL,
 * EXEMPLARY, OR CONSEQUENTIAL DAMAGES (INCLUDING, BUT NOT LIMITED TO,
 * PROCUREMENT OF SUBSTITUTE GOODS OR SERVICES; LOSS OF USE, DATA, OR
 * PROFITS; OR BUSINESS INTERRUPTION) HOWEVER CAUSED AND ON ANY THEORY OF
 * LIABILITY, WHETHER IN CONTRACT, STRICT LIABILITY, OR TORT (INCLUDING
 * NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY OUT OF THE USE OF THIS
 * SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY OF SUCH DAMAGE.
 *
 *

Function Documentation

int Vgreen_coulomb	(	Vgreen *	thee,
		int	npos,
		double *	x,
		double *	y,
		double *	z,
		double *	val
	)

Get the Coulomb's Law Green's function (solution to Laplace's equation) integrated over the atomic point charges using direct summation or H. E. Johnston, R. Krasny FMM library (if available).

Returns the potential 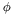$\phi$ defined by

$\phi(r) = \sum_i \frac{q_i}{r_i}$

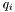where $q_i$ is the atomic charge (in e) and 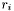$r_i$ is the distance to the observation point 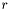$r$ . The potential is scaled to units of V.

Author:: Nathan Baker

Parameters:

	thee	Vgreen object
	npos	The number of positions to evaluate
	x	The npos x-coordinates
	y	The npos y-coordinates
	z	The npos z-coordinates
	val	The npos values

Returns:: 1 if successful, 0 otherwise

References sVgreen::alist, sVgreen::np, sVgreen::qp, Valist_getNumberAtoms(), Vgreen_coulomb_direct(), sVgreen::vmem, Vunit_ec, Vunit_eps0, Vunit_pi, sVgreen::xp, sVgreen::yp, and sVgreen::zp.

Here is the call graph for this function:

int Vgreen_coulomb_direct	(	Vgreen *	thee,
		int	npos,
		double *	x,
		double *	y,
		double *	z,
		double *	val
	)

Get the Coulomb's Law Green's function (solution to Laplace's equation) integrated over the atomic point charges using direct summation.

Returns the potential 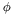$\phi$ defined by

$\phi(r) = \sum_i \frac{q_i}{r_i}$

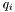where $q_i$ is the atomic charge (in e) and 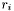$r_i$ is the distance to the observation point 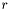$r$ . The potential is scaled to units of V.

Author:: Nathan Baker

Parameters:

	thee	Vgreen object
	npos	The number of positions to evaluate
	x	The npos x-coordinates
	y	The npos y-coordinates
	z	The npos z-coordinates
	val	The npos values

Returns:: 1 if successful, 0 otherwise

References sVgreen::alist, Valist_getAtom(), Valist_getNumberAtoms(), Vatom_getCharge(), Vatom_getPosition(), Vunit_ec, Vunit_eps0, and Vunit_pi.

Referenced by Vgreen_coulomb().

Here is the call graph for this function:

int Vgreen_coulombD	(	Vgreen *	thee,
		int	npos,
		double *	x,
		double *	y,
		double *	z,
		double *	pot,
		double *	gradx,
		double *	grady,
		double *	gradz
	)

Get gradient of the Coulomb's Law Green's function (solution to Laplace's equation) integrated over the atomic point charges using either direct summation or H. E. Johnston/R. Krasny FMM library (if available).

Returns the field 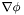$\nabla \phi$ defined by

$\nabla \phi(r) = \sum_i \frac{q_i}{r_i}$

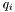where $q_i$ is the atomic charge (in e) and 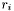$r_i$ is the distance to the observation point 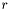$r$ . The field is scaled to units of V/Å.

Author:: Nathan Baker

Parameters:

	thee	Vgreen object
	npos	The number of positions to evaluate
	x	The npos x-coordinates
	y	The npos y-coordinates
	z	The npos z-coordinates
	pot	The npos potential values
	gradx	The npos gradient x-components
	grady	The npos gradient y-components
	gradz	The npos gradient z-components

Returns:: 1 if successful, 0 otherwise

References sVgreen::alist, sVgreen::np, sVgreen::qp, Valist_getNumberAtoms(), Vgreen_coulombD_direct(), sVgreen::vmem, Vunit_ec, Vunit_eps0, sVgreen::xp, sVgreen::yp, and sVgreen::zp.

Here is the call graph for this function:

int Vgreen_coulombD_direct	(	Vgreen *	thee,
		int	npos,
		double *	x,
		double *	y,
		double *	z,
		double *	pot,
		double *	gradx,
		double *	grady,
		double *	gradz
	)

Get gradient of the Coulomb's Law Green's function (solution to Laplace's equation) integrated over the atomic point charges using direct summation.

Returns the field 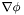$\nabla \phi$ defined by

$\nabla \phi(r) = \sum_i \frac{q_i}{r_i}$

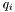where $q_i$ is the atomic charge (in e) and 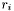$r_i$ is the distance to the observation point 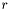$r$ . The field is scaled to units of V/Å.

Author:: Nathan Baker

Parameters:

	thee	Vgreen object
	npos	The number of positions to evaluate
	x	The npos x-coordinates
	y	The npos y-coordinates
	z	The npos z-coordinates
	pot	The npos potential values
	gradx	The npos gradient x-components
	grady	The npos gradient y-components
	gradz	The npos gradient z-components

Returns:: 1 if successful, 0 otherwise

References sVgreen::alist, Valist_getAtom(), Valist_getNumberAtoms(), Vatom_getCharge(), Vatom_getPosition(), Vunit_ec, and Vunit_eps0.

Referenced by Vgreen_coulombD().

Here is the call graph for this function:

Vgreen* Vgreen_ctor ( Valist * alist )

Construct the Green's function oracle.

Author:: Nathan Baker

Parameters:

alist

Atom (charge) list associated with object

Returns:: Pointer to newly allocated Green's function oracle

References Vgreen_ctor2().

Referenced by Vfetk_PDE_initAssemble().

Here is the call graph for this function:

int Vgreen_ctor2	(	Vgreen *	thee,
		Valist *	alist
	)

FORTRAN stub to construct the Green's function oracle.

Author:: Nathan Baker

Parameters:

	thee	Pointer to memory allocated for object
	alist	Atom (charge) list associated with object

Returns:: 1 if successful, 0 otherwise

References sVgreen::alist, and sVgreen::vmem.

Referenced by Vgreen_ctor().

void Vgreen_dtor ( Vgreen ** thee )

Destruct the Green's function oracle.

Author:: Nathan Baker

Parameters:

thee

Pointer to memory location for object

References Vgreen_dtor2().

Referenced by Vfetk_PDE_initAssemble().

Here is the call graph for this function:

void Vgreen_dtor2 ( Vgreen * thee )

FORTRAN stub to destruct the Green's function oracle.

Author:: Nathan Baker

Parameters:

thee

Pointer to object

References sVgreen::vmem.

Referenced by Vgreen_dtor().

Valist* Vgreen_getValist ( Vgreen * thee )

Get the atom list associated with this Green's function object.

Author:: Nathan Baker

Parameters:

thee

Vgreen object

Returns:: Pointer to Valist object associated with this Green's function object

References sVgreen::alist.

int Vgreen_helmholtz	(	Vgreen *	thee,
		int	npos,
		double *	x,
		double *	y,
		double *	z,
		double *	val,
		double	kappa
	)

Get the Green's function for Helmholtz's equation integrated over the atomic point charges.

Returns the potential 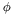$\phi$ defined by

$\phi(r) = \sum_i \frac{q_i e^{-\kappa r_i}}{r_i}$

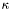where $\kappa$ is the inverse screening length (in Å) 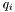$q_i$ is the atomic charge (in e), and 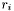$r_i$ r_i is the distance from atom 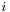$i$ to the observation point 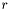$r$ . The potential is scaled to units of V.

Author:: Nathan Baker

Bug:: Not implemented yet

Note:: Not implemented yet

Parameters:

	thee	Vgreen object
	npos	Number of positions to evaluate
	x	The npos x-coordinates
	y	The npos y-coordinates
	z	The npos z-coordinates
	val	The npos values
	kappa	The value of 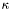$\kappa$ (see above)

Returns:: 1 if successful, 0 otherwise

int Vgreen_helmholtzD	(	Vgreen *	thee,
		int	npos,
		double *	x,
		double *	y,
		double *	z,
		double *	gradx,
		double *	grady,
		double *	gradz,
		double	kappa
	)

Get the gradient of Green's function for Helmholtz's equation integrated over the atomic point charges.

Returns the field 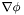$\nabla \phi$ defined by

$\nabla \phi(r) = \nabla \sum_i \frac{q_i e^{-\kappa r_i}}{r_i}$

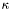where $\kappa$ is the inverse screening length (in Å). 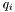$q_i$ is the atomic charge (in e), and 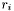$r_i$ r_i is the distance from atom 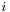$i$ to the observation point 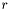$r$ . The potential is scaled to units of V/Å.

Author:: Nathan Baker

Bug:: Not implemented yet

Note:: Not implemented yet

Parameters:

	thee	Vgreen object
	npos	The number of positions to evaluate
	x	The npos x-coordinates
	y	The npos y-coordinates
	z	The npos z-coordinates
	gradx	The npos gradient x-components
	grady	The npos gradient y-components
	gradz	The npos gradient z-components
	kappa	The value of 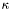$\kappa$ (see above)

Returns:: int 1 if sucessful, 0 otherwise

unsigned long int Vgreen_memChk ( Vgreen * thee )

Return the memory used by this structure (and its contents) in bytes.

Author:: Nathan Baker

Parameters:

thee

Vgreen object

Returns:: The memory used by this structure and its contents in bytes

References sVgreen::vmem.

Vgreen class

Data Structures

Files

Typedefs

Functions

Detailed Description

Function Documentation